What are t-tests? A guide to analyzing survey results
Learn how to test if there are statistically significant differences in your data.

While anyone can see the difference between two numbers, finding out whether that difference is statistically significant can take more work.
Let’s say you’ve run a customer satisfaction survey at work. Your boss wants to analyze if men give your company a lower Net Promoter Score℠ (NPS) than women.
In the data, you see that the average rating from male respondents was 9, compared to an average score of 12 from female respondents. How can you determine if nine is significantly different from 12? This is where t-tests come in.
In this article, we’ll define t-tests and their use cases, share examples of t-tests, and explain how to interpret your results.
T-tests explained
What are t-tests?
A t-test compares two numbers to determine if their difference is statistically significant. This test helps determine if observed differences are statistically significant or due to chance. It is especially useful with small sample sizes.
The test calculates a t-value, which is compared to a critical value from the t-distribution to determine statistical significance. Often used in hypothesis testing, t-tests can be highly valuable for determining if two groups differ in a measured characteristic.
Testing for statistical significance is common in concept testing and product testing. In concept testing, AB tests are commonly used to determine if one ad concept performs better than another. Similarly, product testing can determine if a product will hold its own when launched into the market.
3 t-test formulas
Various types of t-tests use specific formulas to calculate statistically significant differences, with the two-sample t-test being the most common. The formula for this t-test is:
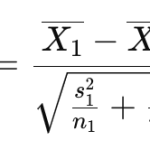
Here are the formulas for the one-sample t-test and paired t-test:

In both the one-sample and paired t-tests, the calculated t-value is compared to a critical value from the t-distribution to assess significance.
When to use a t-test
How do you know when to use a t-test? There are several times when you might choose to utilize a t-test after gathering data from a survey or questionnaire, including:
- Comparing means. You can use a t-test to determine if there is a significant difference between the means of two groups or a sample and a known value.
- Small sample size. When your sample size is small, it may benefit you to use a t-test. A good rule of thumb is to use a t-test if the sample size is less than 30 and the population standard deviation is unknown.
3 common types of t-tests and when to use them
There are three types of t-tests commonly used by researchers. These t-tests serve different purposes that we’ll explain below.
1. One-sample t-test
The one-sample test looks at whether the mean (aka average) of data from one group (in this case, the overall NPS) is different from a value you specify.
Example: Your company’s goal is to have an NPS significantly higher than the industry standard 5. Your company’s latest survey puts its NPS at 10. Is an NPS of 10 significantly higher than the industry standard of 5?
2. Two-sample t-test
Two-sample t-tests examine whether the means of two independent groups are significantly different from one another.
Example: Your hypothesis is that men give your company a lower NPS than women. The average NPS from male respondents is 9, while the average score from women is 12. Is 9 significantly different from 12?
3. Paired t-test
This test is for when you give one group of people the same survey twice. A paired t-test lets you know if the mean changed between the first and second surveys.
Example: You surveyed the same group of customers twice: once in April and a second time in May, after they had seen an ad for your company. Did your company’s NPS change after customers saw the ad?
How to conduct a t-test in 4 steps (with example)

There are four steps to performing a t-test.
This section walks through the four steps using the NPS ratings example from the beginning:
Your hypothesis is that men give a lower NPS to your company than women. The average NPS from men is 9, while the average score for women is 12. Is 9 significantly different from 12? This is an example for performing a two-sample t-test.
Let’s dive into the steps and t-test example.
1. Calculate the t-statistic
Each type of t-test has a different formula for calculating the t-statistic. For this example, we’ll use the two-sample t-test formula where:
- t is the t-statistic
- x1 is the average NPS for men → 9
- x2 is the average for women → 12
- n1 is the number of men who responded to the NPS question → say 20 men responded to the survey
- n2 is the number of women → 23 women responded
- s1 is the standard deviation of the NPS for men → say the calculated standard deviation is 12.48
- s2 is the standard deviation of the NPS for women → the calculated standard deviation is 10.51
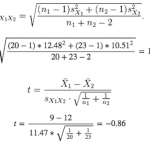
You’ll probably be conducting the t-tests in a spreadsheet or statistical program (like Excel or SPSS). However, if you’d like to do the math by hand, the formulas for the other two types of t-tests are included below.

2. Calculate the degrees of freedom
Degrees of freedom are the number of ways the mean could vary. In this case, the degrees of freedom are the number of NPS ratings you could have in a given group of respondents. Similar to the t-statistic, the formula for degrees of freedom will vary depending on the type of t-test you perform.
This formula must be used to determine degrees of freedom in two-sample t-tests.
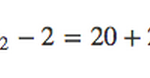
3. Determine the critical value
The critical value is the threshold at which the difference between two numbers is considered statistically significant.
According to this table, for a two-tailed test with an alpha level of 0.05 at 41 degrees of freedom, the critical value is 2.02. Note that most analysts use a two-tailed test instead of a one-tailed test because it’s more conservative.
For more information on the differences between one-tailed and two-tailed tests, check out this video from Khan Academy.
4. Compare the absolute value of the t-statistic to the critical value
If your t-statistic is larger than your critical value, your difference is significant. If your t-statistic is smaller, then your two numbers are, statistically speaking, indistinguishable.
In our example, the absolute value of the t-statistic is 0.86, which is not larger than the critical value of 2.02, so you can conclude that men do not give significantly lower NPS ratings than women.
How to interpret t-test results
When running a t-test, you will need to interpret the results using three components: the t-value, the degrees of freedom (df), and the p-value.
Let’s explore these values and how to interpret the results of your t-test.
T-value: The t-value is the size of the difference relative to any variation in the data. A high t-value indicates a greater difference between the group means relative to the variability. A low t-value indicates a lesser difference between the group means which implies that the difference is likely by chance.
Degrees of freedom (df): The degrees of freedom refer to the values that are free to vary when calculating a statistic. This number of values is used to reference the right critical values.
P-value: P-value is the value that represents if an observed difference is statistically significant or not. The p-value is the probability of observing the test statistic under the null hypothesis (i.e., no difference between groups). The p-value threshold is typically 0.05 (5%).
- P-value ≤ 0.05: This means you reject the null hypothesis and deem the results statistically significant.
- P-value > 0.05: This means the difference is not statistically significant, and you fail to reject the null hypothesis for an alternative hypothesis.
Additionally, t-test results may sometimes also present a confidence interval (CI) for the difference between the means. The confidence interval shares a range of values that the true value is likely to fall within. A significant difference between groups is likely when the CI does not include zero.
Presenting your t-test results
Done correctly, your data analysis could lead marketing efforts or product development. However, you must get buy-in from stakeholders first. For this reason, you must take extra care in presenting your data to ensure stakeholders understand the significance of your findings and next steps.
You should include these five components in your t-test results presentation:
- State the purpose. First, share why you ran a t-test and the goal of the test. For example, explain you used a t-test to prove a statistically significant difference between the means of two groups in your survey results.
- Share descriptive stats. Next, highlight the mean and standard deviation for each group being evaluated. This gives stakeholders the necessary context to understand the differences observed. You should also disclose the sample sizes for each group as further context.
- Present the t-test results. Then, share the t-value, degrees of freedom (df), p-value, and the confidence interval analysis (if you did one).
- Share your findings. Lastly, it’s time to share your findings with stakeholders. Briefly discuss whether or not the difference was statistically significant and what that means regarding your hypothesis or research question.
- Offer next steps. Explain to stakeholders what your research findings mean for the company. Share the next steps on how your results could impact business decisions.
T-test FAQs
- T-tests vs. ANOVA
- Z-tests vs. t-tests
Build better surveys for analysis with SurveyMonkey
T-tests are used to determine if the difference in the means of two sample groups is statistically significant. You can use t-tests during survey data analysis to help share the reliability of your data.
SurveyMonkey allows you to streamline the process of creating and sending surveys to sample groups for your organization’s research needs. With SurveyMonkey, you can build market research surveys and questionnaires from scratch or tap into our broad selection of over 400 survey templates.
Get started collecting survey data for analysis today to help your organization make better decisions for growth. Create a free account today.
Net Promoter Score is a trademark of Bain & Company, Inc., Satmetrix Systems, Inc. and F. Reichheld.
Discover more resources

The insights manager's secret to delivering quality research
Insights managers can use this toolkit to help you deliver compelling, actionable insights to support stakeholders and reach the right audiences.

How industry leaders use employee and customer feedback to drive innovation
How to use customer and employee feedback to drive innovation with insights from LinkedIn, FranklinCovey, and Hornblower.

How data at work impacts the employee experience
New research on the role of data on the employee experience; how it impacts decision making, worker confidence, and trust in teammates and leaders

3 workplace trends that will reshape today’s workforce
New research on workplace trends and how employees are balancing personal time, working from home, and the gap in remote and in-office work